本文并不按照难度和自然推导顺序整理,而是已补充的方式后置部分基础知识.
参考书籍
《材料热力学》第三版.郝士明,蒋敏,李洪晓编著. 北京:化学工业出版社,2020.12
ISBN 978-7-122-38304-4
纯金属空位浓度推导
平衡状态下空位浓度推导
在某一温度下,无空位状态的Gibbs自由能为$G^0$,有空位为$G^V$,则空位引起的Gibbs自由能变为
$$ \Delta G=G^V-G^0 $$
假设n个空位之间无相互作用,每个空位增加的内能u线性叠加,则
$$ \Delta U=nu $$
对于凝聚态,认为$\Delta U\approx \Delta H$,则$\Delta H = nu$.
若纯金属的原子总数为N,引入n个空位后的微观组态数为
$$ W^V=\frac{\left(N+n\right)!}{N!n!} $$
利用Boltzmann方程
$$ S=k\ln{W} $$
熵变$\Delta S$为
$$ \Delta S=S^V-S^0=k\ln{W^V} $$
在N足够大时,可以用Stirling公式计算阶乘的对数
$$ \ln{\left(N!\right)}=N\ln{N}-N $$
$$ \begin{aligned} \Delta S &=k\left[\left(N+n\right)\ln{\left(N+n\right)}-N\ln{N}-n\ln{n}\right] \\ &=-k\left[N\ln{\frac{N}{N+n}}+n\ln{\frac{n}{N+n}}\right] \end{aligned} $$
而
$$ \Delta G=\Delta H-T\Delta S=nu+kT\left[N\ln{\frac{N}{N+n}}+n\ln{\frac{n}{N+n}}\right] $$
对Gibbs自由能的影响是,存在一定数量的空位$n^*$,此时取得Gibbs自由能的最小值. 可以由下式求得
$$ \begin{aligned} \frac{{\rm d}\Delta G}{{\rm d}n}&=0 \\ U+kT\left[\ln{n}-\left(N+n\right)\right]&=0 \\ \ln{\frac{n}{N+n}}&=-\frac{u}{kT} \end{aligned} $$
若将$\frac{n}{N+n}$定义为空位浓度$X_V$,则可以表示为
$$ X_V=\exp{\left(-\frac{u}{kT}\right)} $$
应当注意到,我们在推导时使用了很多简化近似.
Gibbs自由能的引入
热力学第二定律告诉我们,一个孤立系统总是由熵低的状态向熵高的状态变化,平衡状态则是具有最大熵的状态. 这可以表示成下面的公式:
$$ \left({\rm d}S\right)_{is}\geq0 $$
接下来考察一个孤立系统,包括A和比A热容量大的多的$A^\prime$. $A^\prime$在释放极小的$\delta Q^{A^\prime-A}$后T、P不发生变化.因此$A^\prime$的熵变为:
$$ {\rm d}S_{A^\prime}=-\frac{\delta Q^{A^\prime-A}}{T} $$
而对于A,由热力学第一定律得到
$$ {\rm d}U_A=\delta Q^{A^\prime-A}-p{\rm d}V $$
$A^\prime$的熵变可以写成
$$ {\rm d}S_{A^\prime}=-\frac{{\rm d}U_A+p{\rm d}V_A}{T} $$
对于两者构成的孤立系统熵变为:
$$ {\rm d}S_{A+A^\prime}={\rm d}S_A+{\rm d}S_{A^\prime} $$
进一步可以写成
$$ {\rm d}S_{A+A^\prime}=-\frac{{\rm d}U_A+p{\rm d}V_A-T{\rm d}S_A}{T} $$
至此孤立系统的熵变仅由A的状态函数表示. 我们令
$$ G=U+pV-TS $$
则在等温等压条件下有
$$ {\rm d}G\leq0 $$
注意此处符号. Gibbs自由能为了形成判据,形式由数学限定,其本身只是几种状态函数的组合,只有在特定条件下才有特定含义. 在等温等压条件下,平衡态的一般条件便成为
$$ {\rm d}G=0\ \text{or}\ G=\min $$
热力学基本关系
熵(Entropy)是在研究卡诺循环、热机效率中提出的,旨在将过程量Q纳入状态函数. 对于可逆过程有
$$ {\rm d}S=\frac{\delta Q_\text{rev}}{T}\ \text{or}\ \delta Q_\text{rev}=T{\rm d}S $$
在只有体积功时,Gibbs自由能和Helmholtz自由能的微分形式分别能写成
$$ {\rm d}G=V{\rm d}p-S{\rm d}T $$
$$ {\rm d}F=-p{\rm d}V-S{\rm d}T $$
在5个状态函数中,最为基本的是U和S,具有明确的物理意义. 而引入H、G、F用于方便计算. 其中U和H主要解决能量计算问题,S、G、F主要解决过程方向性的问题.
Maxwell关系
Maxwell关系基于混合偏导数交换定理(Clairaut 定理或 Schwarz 定理).
定理(Clairaut / Schwarz):
设函数 $f\left(x,y\right)$ 在点 $\left(x_0,y_0\right)$ 的某邻域内具有二阶偏导数,且这些二阶偏导数连续,则:
$$ \frac{\partial^2 f}{\partial x\partial y}\left(x_0,y_0\right)=\frac{\partial^2 f}{\partial y\partial x}\left(x_0,y_0\right) $$
推导不再给出.
对于
$$ {\rm d}H=T{\rm d}S+V{\rm d}p $$
同时有
$$ {\rm d}H=\left(\frac{\partial H}{\partial S}\right)_p{\rm d}S+\left(\frac{\partial H}{\partial p}\right)_S{\rm d}p $$
可以得到一组对应系数关系式,如
$$ \left(\frac{\partial U}{\partial S}\right)_V=\left(\frac{\partial H}{\partial S}\right)_p=T $$
再次利用上面的数学结论,可以得到另一组关系式:
$$ \left(\frac{\partial T}{\partial p}\right)_S=\left(\frac{\partial V}{\partial S}\right)_p $$
| 势函数 $f$ | 微分表达式 $df$ | 麦克斯韦关系 | 自然变量 | 热力学条件 |
|---|---|---|---|---|
| $S(U, V)$ | $dS = \frac{1}{T} dU + \frac{P}{T} dV$ | $\left( \frac{\partial (1/T)}{\partial V} \right)_U = \left( \frac{\partial (P/T)}{\partial U} \right)_V$ | $U, V$ | 孤立系统,最大熵原理 |
| $U(S, V)$ | $dU = T\,dS - P\,dV$ | $\left( \frac{\partial T}{\partial V} \right)_S = -\left( \frac{\partial P}{\partial S} \right)_V$ | $S, V$ | 定熵、定体积过程 |
| $H(S, P)$ | $dH = T\,dS + V\,dP$ | $\left( \frac{\partial T}{\partial P} \right)_S = \left( \frac{\partial V}{\partial S} \right)_P$ | $S, P$ | 定熵、定压过程 |
| $F(T, V)$ | $dF = -S\,dT - P\,dV$ | $\left( \frac{\partial S}{\partial V} \right)_T = \left( \frac{\partial P}{\partial T} \right)_V$ | $T, V$ | 定温、定体积过程 |
| $G(T, P)$ | $dG = -S\,dT + V\,dP$ | $\left( \frac{\partial S}{\partial P} \right)_T = -\left( \frac{\partial V}{\partial T} \right)_P$ | $T, P$ | 定温、定压过程 |
万事俱备,上面的证明就简单了.
单组元材料的相平衡
晶体定容热容推导
Einstein 热容理论
1907年 Albert Einstein应用量子理论解释了晶体的振动热容. 他认为
- 晶体自热力学零度起的吸热升温过程就是各谐振子以量子为单位吸收能量的过程
- 每个原子的振动可以用三维坐标来描述,每个原子可以看成3个谐振子
- 各谐振子振动频率相同
现在看来,这3条认为各有各的问题,这在后面会提及.
虽然每个谐振子的振动频率相同,但是能量可以不同,可取一系列不连续的能量值
$$ \varepsilon=\left(n_l+\frac{1}{2}\right)h\nu $$
其中$n_l$为量子数,$h\nu$为一个声子.
将每个谐振子记作
$$ a_1,a_2,a_3,...,a_{3N} $$
当在某一温度下,晶体总共吸收了n个声子的能量,分别记作
$$ k_1,k_2,k_3,...,k_n $$
按照这个思路,在3N个谐振子上分配n个声子的组态数有$\left(3N+n\right)!$个. 但是实际上声子是全同的,真正的不同组态数
$$ W=\frac{\left(3N+n\right)!}{\left(3N \right)!n!} $$
由此引起的熵变和内能变化分别为
$$ \begin{aligned} \Delta S&=-k\left(3N\ln\frac{3N}{3N+n}+n\ln{\frac{n}{3N+n}}\right) \\ \Delta U&=nh\nu \end{aligned} $$
对于我们需要得到的定容热容,我们通过Helmholtz自由能导出. 等体积过程的平衡态出现在Helmholtz自由能的变化值$\Delta F$为最小值时,也就是说,在某一温度,晶体不能吸收任意数量的声子,只有某个声子数能使$\Delta F$成为极小值时,这一声子数才是能够实际吸收的. 可以由下式求出:
$$ \begin{aligned} \frac{{\rm d}\Delta F}{{\rm d}n}&=0 \\ h\nu-kT\left[\ln{\left(3N+n\right)-\ln{n}}\right]&=0 \end{aligned} $$
即
$$ \ln{\frac{n}{3N+n}}=-\frac{h\nu}{kT}\ or\ \frac{n}{3N+n}=\exp{\left(-\frac{h\nu}{kT}\right)} $$
$$ n=\frac{3Nh\nu}{\exp{\left(\frac{h\nu}{kT}\right)}-1} $$
由吸收声子引起的内能变化
$$ \Delta U=nh\nu=\frac{3Nh\nu}{\exp{\left(\frac{h\nu}{kT}\right)-1}} $$
则定容热容可以根据定义求得
$$ \begin{aligned} C_V&=\left(\frac{\partial U}{\partial T}\right)_V =\left\{\frac{\partial\left[U\left(0K \right)+\Delta U\right]}{\partial T}\right\}_V \\ C_V&=\frac{3Nh\nu}{\left(\exp{\frac{h\nu}{kT}-1}\right)^2}\left[\exp{\left(\frac{h\nu}{kT}\right)}\right]\frac{h\nu}{kT^2} \\ C_V&=3R\left(\frac{hv}{kT}\right)^2\frac{\exp{\left(\frac{h\nu}{kT}\right)}}{\left(\exp{\frac{h\nu}{kT}-1}\right)^2} \end{aligned} $$
由于$\frac{h\nu}{k}$的量纲与温度相同,定义其为Einstein特征温度$\Theta_E$,则定容热容可以表示为
$$ C_V=3R\left(\frac{\Theta_E}{T}\right)^2\frac{\exp{\left(\frac{\Theta_E}{T}\right)}}{\left(\exp{\frac{\Theta_E}{T}-1}\right)^2} $$
Einstein定容热容理论无法说明在极低温时的实验数据. Debye对晶体振动热容理论做了修正,其不把各谐振子的振动频率看作相同,也不把各谐振子看作是相互独立的. 在低温下的Debye定容热容为
$$ C_V=1943.8\left(\frac{T}{\Theta_D}\right)^3 $$
这就是温度三次方经验定律,式中$\Theta_D=\frac{h\nu_m}{k}$称为Debye特征温度,$\nu_m$是最大振动频率.
热容与自由能
给出物质在某一温度下的热容C.
$$ C=\lim_{\Delta T\rightarrow0}{\frac{\delta Q}{\Delta T}}=\frac{\delta Q}{{\rm d}T} $$
显然,热容是温度的函数.
由实验获得的热容主要是定压热容$C_p$
$$ C_p=\left(\frac{\partial H}{\partial T}\right)_p $$
而由理论求得的热容首先是定容热容$C_V$
$$ C_V=\left(\frac{\partial U}{\partial T}\right)_V $$
在明确热容后,熵微分就可以写成
$$ {\rm d}S=\frac{C{\rm d}T}{T} $$
以等压条件为例
$$ S_{p}=\int_0^{T}{\frac{C_p}{T}{\rm d}T+S\left(0K\right)} $$
根据热力学第三定律,热力学系统的熵在温度趋近于绝对零度时趋于定值. 而对于完整晶体,这个定值为零. 可以认为单组元相在热力学零度下的熵$S\left(0K\right)=0$. 所以单组元相的Gibbs自由能可以写成
$$ G=\int_{0}^{T}C_{p}{\rm d}T-T\int_0^{T}\frac{C_p}{T}{\rm d}T+H\left(0K\right) $$
对于Helmholtz自由能同理.
由热容计算自由能
前面提到,单组元材料的Gibbs自由能可以利用定压热容$C_p$积分求得
$$ G=\int_{0}^{T}C_{p}{\rm d}T-T\int_0^{T}\frac{C_p}{T}{\rm d}T+H\left(0K\right) $$
在单组元材料中$C_p$最复杂的是$\alpha-Fe$,下面以$\alpha-Fe$为例求$G-H(0K)$
$\alpha-Fe$的定压热容包括下面几个方面. 一是晶格上离子震动的贡献,即振动热容(Vibrating heat capacity) $\left(C^\alpha_p\right)_\text{vib}$; 二是自由电子吸收能量的贡献,即电子热容(Electronic heat capacity) $\left(C^\alpha_p\right)_\text{elr}$; 还有原子磁矩由有序排列变成无序排列的贡献,即磁性热容(Magnetic heat capacity) $\left(C^\alpha_p\right)_\text{mag}$. 这当然没有构成全部,但是一般情况下贡献了绝大部分.
$\alpha-Fe$的等压热容可以写成
$$ C^\alpha_p=\left(C^\alpha_p\right)_\text{vib}+\left(C^\alpha_p\right)_\text{elr}+\left(C^\alpha_p\right)_\text{mag} $$
可以将$\left(C^\alpha_p\right)_\text{vib}$写成
$$ \left(C^\alpha_p\right)_\text{vib}=\left(C^\alpha_V\right)_\text{vib}+\frac{\alpha^2V_mT}{\kappa_T} $$
式中$\left(C^\alpha_V\right)_\text{vib}$可以用Einstein定容热容表达式展开. 最后会对该式进行解释.
电子热容可以表示为
$$ \left(C^\alpha_p\right)_\text{elr}=\gamma T $$
式中$\gamma$为电子热容系数.
磁性热容与温度的关系是最复杂的,这里采用最简单的一种解析式,Ising模型描述的二维简单立方晶格的磁性热容
$$ \left(C^\alpha_p\right)_\text{mag}=R\frac{x^2}{\cosh^2{x}-\frac{x}{\tanh{x}}} $$
式中$R$为气体常数,$x=\frac{T_C}{T}\sigma$;$T_C$是Curie温度,$\sigma=\tanh{\left(\frac{T_C}{T}\sigma\right)}$. 还有很多描述磁性转变的模型,但是都难以准确的与实验结果达到一致. 即使是形如本式的简单表达式,也是无法积分的,在计算时还是采用磁性热容的实测结果经数值积分求得. 可以将此部分与最后的磁性转变部分对照观看.
分别带入Gibbs自由能表达式算出焓项与熵项即可.
铁的特殊密排转变
这种理论可以解释纯$\alpha-Fe$到$\gamma-Fe$的密排转变.
而对于一般金属,由于
$$ \left(\frac{\partial H}{\partial V}\right)_T=T\left(\frac{\partial S}{\partial V}\right)_T+V\left(\frac{\partial p}{\partial V}\right)_T $$
对于凝聚态而言
$$ \left(\frac{\partial H}{\partial V}\right)_T \approx T\left(\frac{\partial S}{\partial V}\right)_T = T\left(\frac{\partial p}{\partial T}\right)_V > 0 $$
这表明,对于同一金属温度一定时,疏排结构的焓大于密排结构;
另有
$$ \left(\frac{\partial S}{\partial V}\right)_T=\left(\frac{\partial p}{\partial T}\right)_V > 0 $$
这表明,对于同一金属温度一定时,疏排结构的熵大于密排结构.
结合这两点可知,在低温时,熵项对Gibbs自由能的贡献较小,G主要取决于H,此时密排结构的焓比较小,更稳定;在高温时,熵项对Gibbs自由能的贡献很大,G主要取决于TS,此时疏排结构的熵比较大,Gibbs自由能更小,更稳定.
Cp与Cv的差值
我们先推导热容差的一般公式. 由
$$ C_p-C_V=T\left[\left(\frac{\partial S}{\partial T}\right)_p-\left(\frac{\partial S}{\partial T}\right)_V\right] $$
将$\left(\frac{\partial S}{\partial T}\right)_p$用链式法则展开
$$ \left(\frac{\partial S}{\partial T}\right)_p=\left(\frac{\partial S}{\partial T}\right)_V+\left(\frac{\partial S}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_p $$
由Maxwell关系知
$$ \left(\frac{\partial S}{\partial V}\right)_T=\left(\frac{\partial p}{\partial T}\right)_V $$
因此
$$ C_p-C_V=T\left(\frac{\partial p}{\partial T}\right)_V\left(\frac{\partial V}{\partial T}\right)_p $$
再引入热膨胀系数$\alpha$和等温压缩率$\kappa_T$
$$ \begin{aligned} \alpha&=\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_p\Rightarrow \left(\frac{\partial V}{\partial T}\right)_p=\alpha V\\ \kappa_T&=-\frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_T\Rightarrow\left(\frac{\partial p}{\partial T}\right)_V=\frac{\alpha}{\kappa_T} \end{aligned} $$
可以通过写出${\rm d}V$来得到$\frac{{\rm d}p}{{\rm d}T}$.
至此
$$ C_p-C_V=\frac{TV\alpha^2}{\kappa_T} $$
单元材料的两相平衡
既然是两相平衡,材料在等温等压下由一项变为另一项,Gibbs自由能的变化为0. 在压力$P_1$和温度$T_1$下,
$$ G^\alpha_m=G^\beta_m $$
若使压力改变${\rm d}p$、温度相应的改变${\rm d}T$之后两相仍然呈平衡,此时显然有
$$ {\rm d}G^\alpha={\rm d}G^\beta $$
由微分关系得
$$ \frac{{\rm d}p}{{\rm d}T}=\frac{S^\alpha_m-S^\beta_m}{V^\alpha_m-V^\beta_m}=\frac{\Delta S^{\beta\rightarrow\alpha}_m}{\Delta V^{\beta\rightarrow\alpha}_m} $$
对于等温等压下的可逆相变,相变温度为$T$时
$$ \frac{{\rm d}p}{{\rm d}T}=\frac{\Delta H^{\alpha\rightarrow\beta}_m}{T\Delta V^{\alpha\rightarrow\beta}_m} $$
这就是Clapeyron方程,适用于任何单组元材料的两相平衡.
对于凝聚态相变而言,压力变化不大时
$$ \frac{{\rm d}p}{{\rm d}T}=\text{const.} $$
对有气相参加的两相平衡,压力改变时$\Delta V_m$比较大,与气相体积相比,凝聚态的体积可以忽略,即
$$ \Delta V^{L(S)\rightarrow G}_m=V^G_m-V^{L(S)}_m= V^G_m $$
对于气体有
$$ V^G_m=\frac{RT}{p} $$
因此可以改写Clapeyron方程为
$$ \frac{{\rm d}p}{{\rm d}T}=\frac{\Delta H_m}{RT^2}p\ or\ \frac{{\rm d} \ln{p}}{{\rm d}T}=\frac{\Delta H_m}{RT^2} $$
称为Clausius-Clapeyron方程.
积分得到
$$ \ln{p}=-\frac{\Delta H_m}{RT}+C $$
若令$C=\ln{A}$
$$ p=A\exp{\left(-\frac{\Delta H_m}{RT}\right)} $$
这表明,凝聚态与气相之间的$p-T$平衡呈指数关系. 凝聚态之间的平衡(除去铁磁-顺磁转变等没有明显潜热和体积突变等的二级相变)遵循Clapeyron方程,呈线性关系.
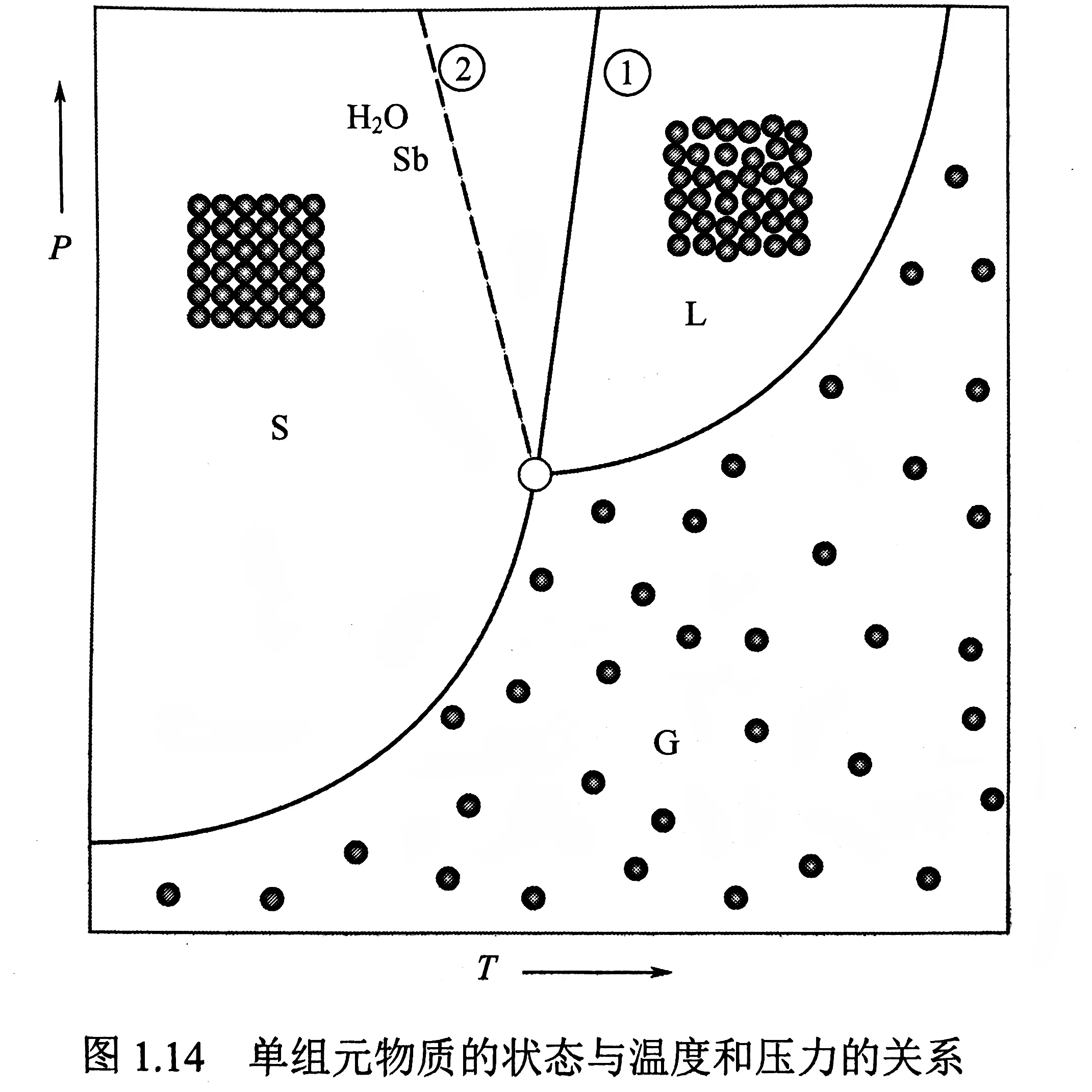
对于绝大部分单组元材料,$\Delta H_m$与$\Delta V_m$是同符号的,在上图中表现为$\textcircled{1}$线 ,而对于少数物质,如$H_2O、Sb、Bi、Si、Ga、Ge$等,在$S\rightarrow L$时是吸热相变却发生体积收缩,在上图中表现为$\textcircled{2}$线.
单组元材料不仅在温度改变时会发生相变,在温度不变而压力发生变化时也会发生相变,比如$\alpha-Fe\rightleftharpoons\varepsilon-Fe$,该相平衡压力在$8至13GPa$之间.
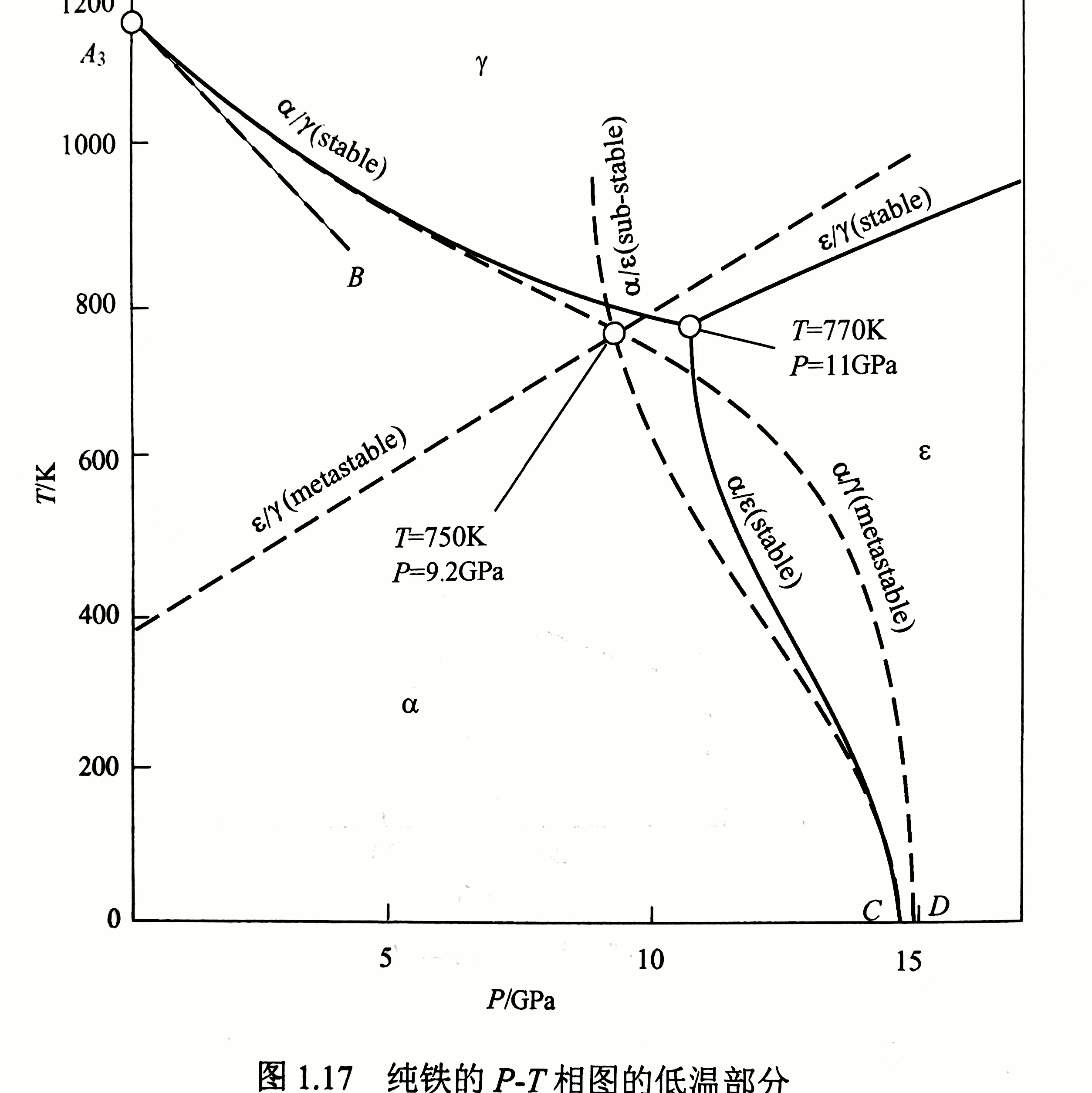
注意到,三个两相平衡线都并不是直线,是因为在这样的温度压力范围内$\Delta H_m、\Delta V_m$都不是定值.
Gibbs-Helmholtz方程
单组元材料在相平衡温度以外时,两相自由能不同,这个自由能差称为相变自由能. 相变自由能与温度的关系被称为Gibbs-Helmholtz方程. 在定压时求$\Delta G=G^B-G^A$对$T$的偏导
$$ \left[\frac{\partial\left(\Delta G\right)}{\partial T}\right]_p=-S^B+S^A=-\Delta S $$
在温度一定时
$$ \left[\frac{\partial\left(\Delta G\right)}{\partial T}\right]_p=\frac{\Delta G-\Delta H}{T} $$
整理上式得
$$ \left[\frac{\partial\left(\Delta G/T\right)}{\partial T}\right]_p=-\frac{\Delta H}{T^2} $$
通过一些积分小trick可以得到
$$ \frac{\Delta G}{T}=-\int\frac{\Delta H}{T^2}{\rm d}T+I $$
其中
$$ \Delta H=\int\Delta C_p{\rm d}T+\Delta H_0 $$
定压热容可以由实验得到的多项式给出
$$ \Delta H=\Delta H_0+\Delta aT+\frac{\Delta b}{2}T^2-\frac{\Delta c}{T} $$
多项式形式给出的等压热容都是实验测得具有范围的,因此上式也是具有温度范围的,对于不同的温度范围需要不同多项式系数. 那么$\Delta H_0$从何而来呢?当然需要在某个温度得知此时的焓变,代入上式反推即可.
磁性转变的自由能
按照磁化率$\chi=\frac{J}{H}$(J和H分别为磁化强度和磁场强度)可以把材料分别为3类
- $\chi <0$ 抗磁材料,如$Cu、Ag、Zn、Cd、Hg$以及金刚石、$NaCl$等.
- $\chi > 0$ 顺磁材料,如碱金属、碱土金属、大部分过渡金属以及明矾$[KAl(SO_4)_2\cdot12H_2O]$等氧化物.
- $\chi\gg0$ 铁磁材料,如$Fe、Co、Ni$稀土金属以及各种铁氧化体等.
在室温下为铁磁性的金属在超过某一温度(Curie温度)后将变成顺磁性的,自发磁性消失. $\text{铁磁态}\rightleftharpoons\text{顺磁态}$转变并不伴随晶体结构的变化,只是晶体中各个原子的磁矩由有序变为无序排列. 原子的磁矩是由未填满的3d、4f电子壳层中不成对电子的自旋矩引起的. 铁磁性物质的原子磁矩因交换作用而排列成有序状态以降低能量的行为被称为自发磁化(Spontaneous magnetization). 温度的提高将破坏这种有序状态,使磁有序度(Magnetic order parameter)逐渐降低.
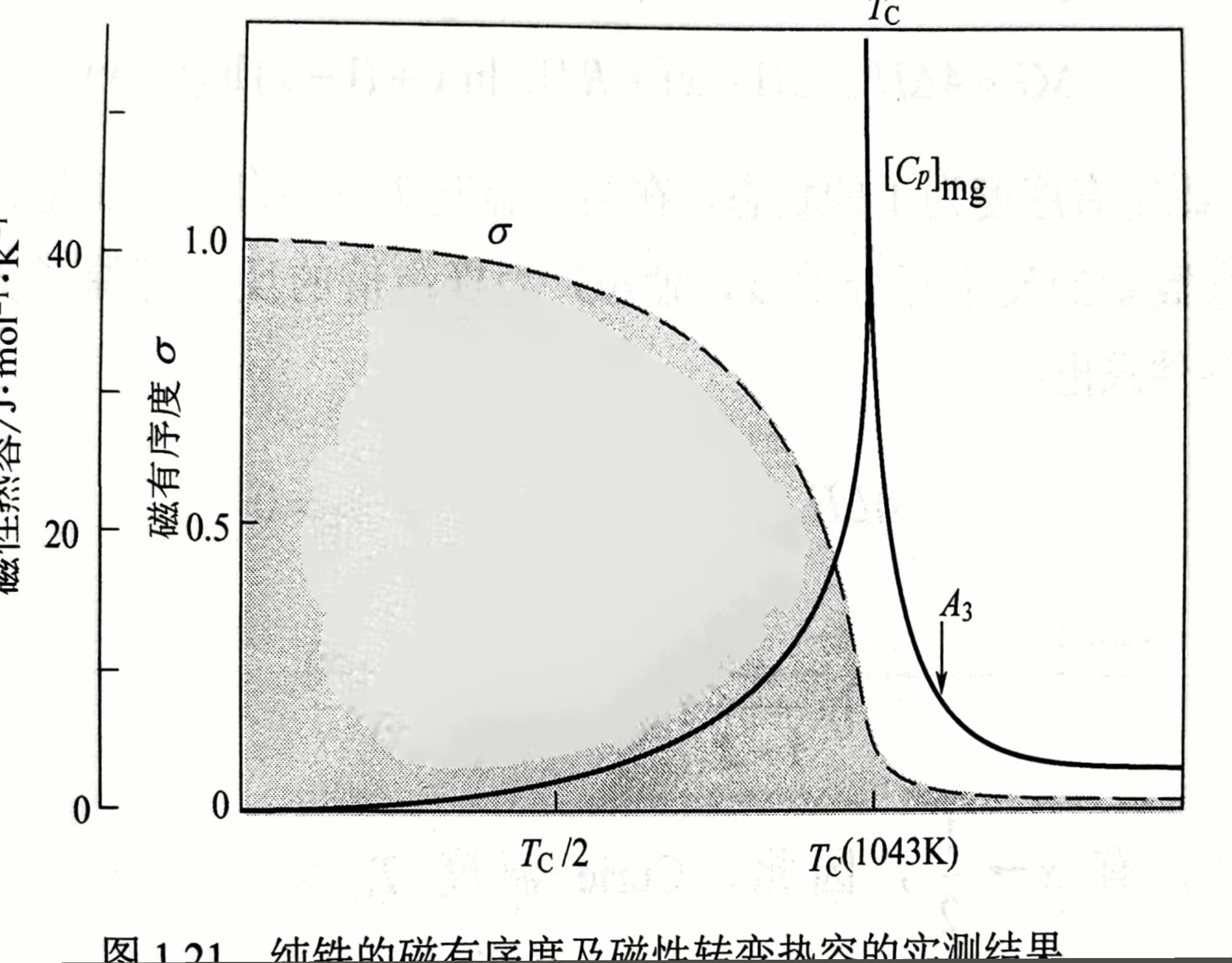
我们可以先研究一个简单模型.
假设晶体中每个原子只有一个不成对电子,构成一个玻尔磁子即磁矩;假设磁矩只有两种取向:平行和反平行;假设部分原子磁矩反平行排列带来的内能增加为$\Delta U$,在凝聚态下$\Delta U\approx H$,若在N个原子组成的晶体中有n个原子的磁矩是反平行排列,令$x=\frac{n}{N}$则
$$ \Delta H=k_mx(1-x)N^2 $$
$k_m$为反平行系数,含义为使一个原子由平行排列变为反平行排列时带来的焓变.
这是一个极大的简化,以至于在该一维模型下甚至不能解释铁磁性. 不过还是有继续下去的必要. 所以不要和上面铁的例子过于比对.
当$x=\frac{1}{2}$时,磁矩有序度为0,焓变达到最大
$$ \Delta H_\text{max}=\frac{1}{4}k_mN^2 $$
代回原式
$$ \Delta H=4\Delta H_\text{max} x(1-x) $$
类似于在空位推导部分做的工作,可以得到反平行排列原子带来的 Boltzmann熵增
$$ \Delta S=-k\left[n\ln{\frac{n}{N}}+(N-n)\ln{\frac{N-n}{N}}\right] $$
若晶体取$1mol$
$$ \Delta S=-R\left[x\ln{x}+(1-x)\ln{(1-x)}\right] $$
代入可得
$$ \Delta G=4\Delta H_\text{max} x(1-x)+RT\left[x\ln{x}+(1-x)\ln{(1-x)}\right] $$
这就是相对于磁矩有序度为1时,在某一温度下的自由能变化.
至于Curie温度等,变形后洛必达即可求出
$$ T_C=\frac{2\Delta H_\text{max}}{R} $$
$$ \Delta G=2RT_C(1-x)x+RT\left[x\ln{x}+(1-x)\ln{(1-x)}\right] $$
在$T_C$温度以上时,金属处于磁矩的完全无序态,此时$x=\frac{1}{2}$
$$ \Delta G^P=\frac{RT_C}{2}-RT\ln{2} $$
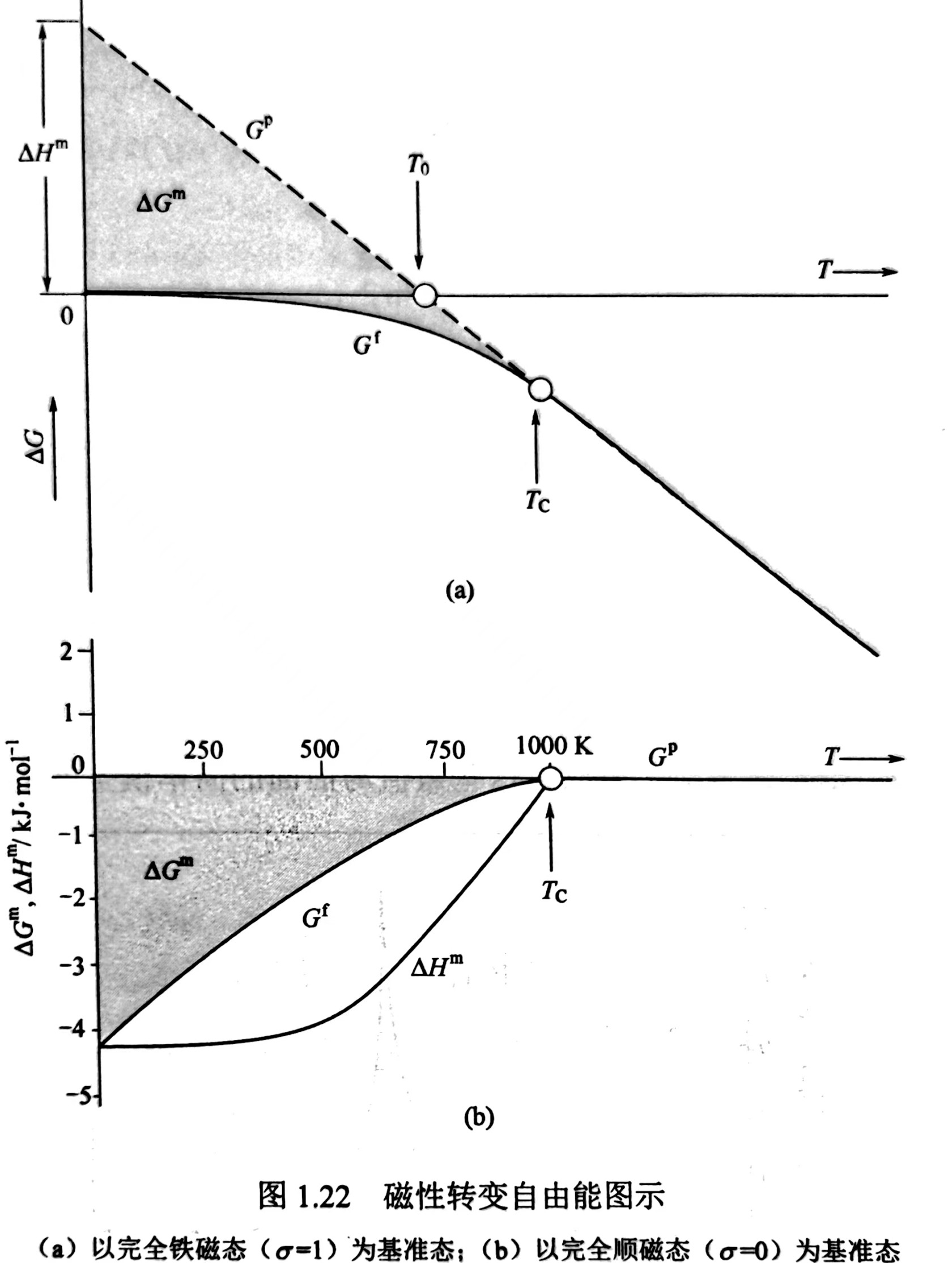
补充说明:上图(a)中$T_0$代表理论对于铁磁材料顺磁态存在的理论最低温度.
评论区(暂无评论)