尚未完成

参考书籍

《材料热力学》第三版.郝士明，蒋敏，李洪晓编著. 北京：化学工业出版社，2020.12
ISBN 978-7-122-38304-4

溶体近似

理想溶体近似

在宏观上，A、B两种组元的分子混合在一起后，既没有热效应也没有体积效应，所形成的溶体即为理想溶体。这种条件很苛刻，不仅要求A、B两种组元具有相同的结构，同时要求A、B两种组元具有相同的晶格常数.

在微观上，要求

$$ u_\text{AB}=\frac{u_\text{AA}+u_\text{BB}}{2} $$

我们由Boltzmann求出混合熵(见上一节)

$$ \Delta S_\text{mix}=-R\left(X_A\ln{X_A}+X_B\ln{X_B}\right) $$

显然在$X_A=X_B=\frac{1}{2}$时混合熵取得最大值.
在这种近似下，摩尔Gibbs自由能可以写成

$$ G_m=X_AG^0_A+X_BG^0_B+RT\left(X_A\ln{X_A}+X_B\ln{X_B}\right) $$

我们对纯组元的热力学函数符号，额外标0以区分.

正规溶体近似

实际合金熔液不可能是理想溶体，上面提出的条件难以或者不可能达成. 在理想溶体的基础上，我们提出正规溶体近似，以针对更普遍的情况进行修正. 该近似修正了摩尔自由能

$$ G^R_m=G^\text{id}_m+\Delta G^E $$

其中

$$ \Delta G^E=X_AX_BI_\text{AB} $$

$I_\text{AB}$称为相互作用能，是由A、B决定的常数：

$$ I_\text{AB}=zN_a\left(u_\text{AB}-\frac{u_\text{AA}+u_\text{BB}}{2}\right) $$

因而得到

$$ G_m=X_AG^0_A+X_BG^0_B+RT\left(X_A\ln{X_A}+X_B\ln{X_B}\right)+X_AX_BI_\text{AB} $$

图示如下

正规溶体摩尔自由能的组成
根据不同大小关系，存在下面9种可能的摩尔Gibbs自由能曲线，部分属于同一情况.
9种正规溶体自由能曲线
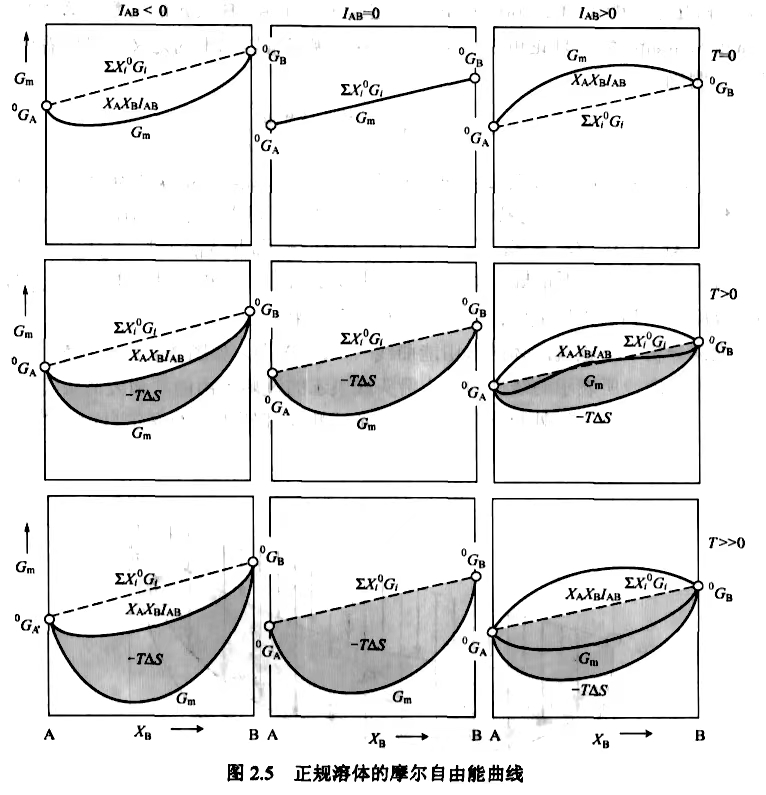
在上述正规溶体近似的情景下，溶体的性质取决于构成溶体组元之间的相互作用.
如果不考虑摩尔Gibbs自由能的线性项，$G_m-X_B$曲线便只取决于温度和$I_\text{AB}$.
固溶体的相互作用能与固溶体中的原子排布及相图
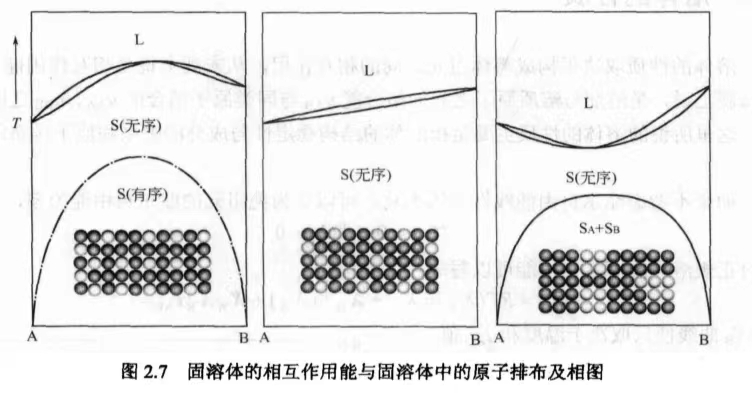
在这种视角下，我们可以认为温度相图反应了原子键合的强弱. 对于$I_\text{AB}=0$的情况（对应中间的图），相线没有极值，固溶体成分具有连续性，不出现原子偏聚. 对于$I_\text{AB}<0$的情况（对应左图），固溶体在低温时原子有序排列，相线在异类原子键分数最大的成分处存在极大值. 对于$I_\text{AB}>0$的情况（对应右图），固溶体在低温时同类原子偏聚，失稳分解（Spinodal decomposition），出现溶解度间隙（Miscibility gap），相线在异类原子键分数最大的成分处存在极小值.

如果不考虑因为偏聚而导致的长程有序或短程有序，偏聚在宏观上表现为无序. 但事实上有很多晶体的相互作用能为正.

混合物的自由能

这里讨论的混合物是由两相混成.
我们通过一点点推导，可以得到

$$ \frac{G_m^M-G_m^\alpha}{G_m^\beta-G_m^\alpha}=\frac{X_B^M-X_B^\alpha}{X_B^\beta-X_B^\alpha} $$

这是一个两点式. 进而得到

$$ G_m^M=\frac{X_B^\beta-X_B^M}{X_B^\beta-X_B^\alpha}G_m^\alpha+\frac{X_B^M-X_B^\alpha}{X_B^\beta-X_B^\alpha}G_m^\beta $$

其中上角标$M$代表混合物，下角标$B$代表以B为基准的成分.
两相混合物的自由能
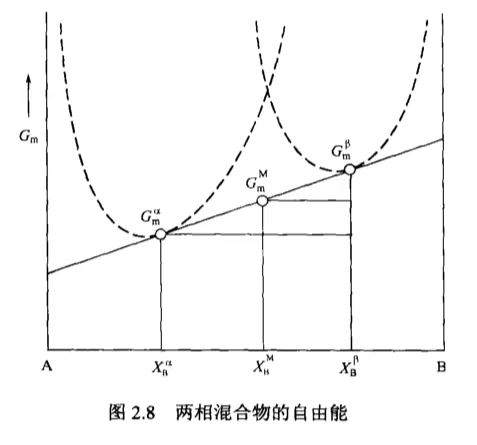
如上图所示（其实这个图画的不大好）. 两条凸函数就是前面提出的正规模型（或理想模型）. 给出的例子是最稳定的公切线，其实可以在可能的范围取点，两相的成分-能量图像可能也不再是两条凸函数，而是两个面积.

Cr-W相图
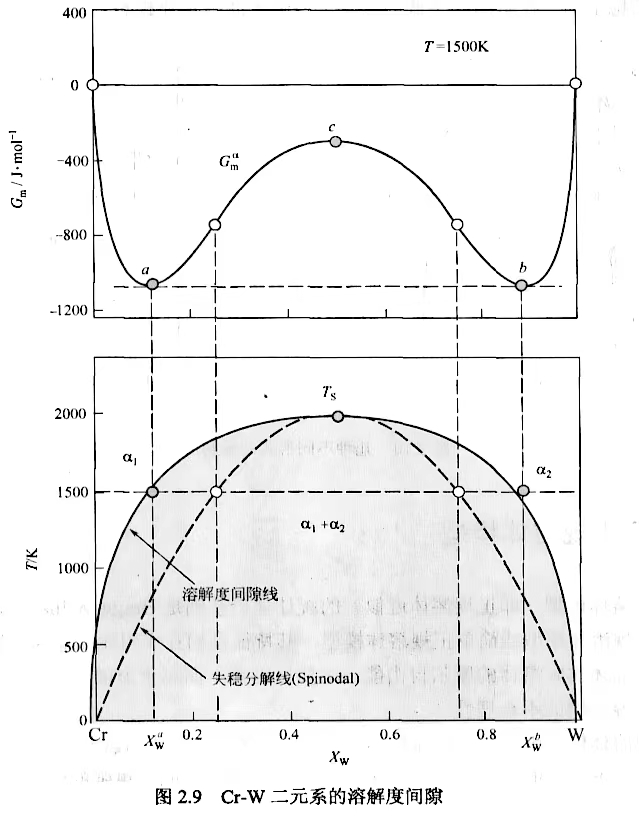
以Cr-W二元系为例，我们应用上面得到的混合律，可以在上图（上，$G_m^\alpha$的Gibbs自由能）中发现，在a、b之间的区段（也就是$\alpha_1$相和$\alpha_2$相之间），混合物的Gibbs自由能是要低于$\alpha$相的. 这也意味着，如果受到比较大的扰动，此时的$\alpha$相可能会分解、析出成混合物. 一种极端情况是，无论受到多么微小的扰动，$\alpha$相都会自发分解成混合物. 可以在上图(上)中标出（表示为白点）. 我们保持自变量不变，把每一温度下的a、b点绘出，得到了溶解度间隙线；同样绘制白点，得到失稳分解线. 两线围成的区域，其物理意义不言自喻.

几种不同形式的溶解度间隙
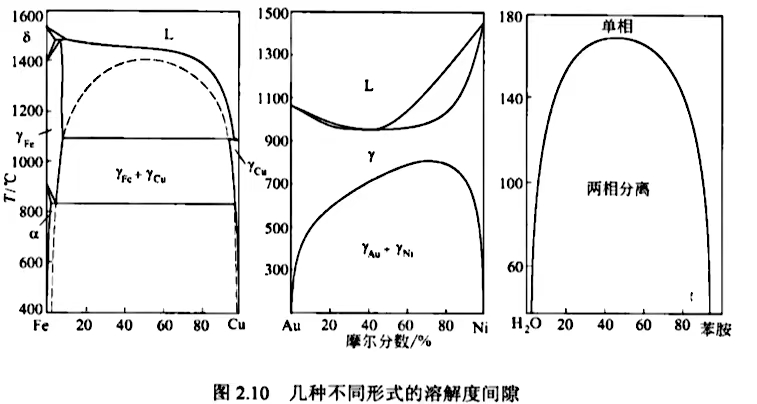
像是Cr-W这样具有完整且对称的固态溶解度间隙的金属系统很少. $H_2O$-苯胺二元系可以视为完整的液态溶解度间隙；Au-Ni系的溶解度间隙不对称，说明该系的相互作用能不是常数，和成分有关；Fe-Cu二元系的溶解度间隙只在$1000^\circ C$稳定，以上以下都是亚稳态.

亚正规溶体模型

在上面的讨论中，我们发现了“特例”（其实讨论的Cr-W才是特例），同时也进行了“善意的忽略”（如“不考虑因为偏聚而导致的长程有序或短程有序“）. 无论是$I_\text{AB}<0$时，还是$I_\text{AB}>0$，都存在短程有序排布，与随机排布相差甚远，实际的混合熵要小于完全随机排布所计算的.

由

$$ I_\text{AB}=zN_a\left(u_\text{AB}-\frac{u_\text{AA}+u_\text{BB}}{2}\right) $$

可知，$I_\text{AB}$为常数的原因是三个结合能为常数. 处于晶格节点上的原子，之间的结合能由原子间距决定，而温度会影响此间距，因而结合能将随温度变化. 此外，溶体成分也会影响原子间距，只有原子尺寸差异不大时才可以忽略.

此外，混合将导致原子振动频率发生变化，因此

$$ G_m=X_AG^0_A+X_BG^0_B+... $$

上式的线性部也不再成立.

倘若坚持使用

$$ G_m=X_AG^0_A+X_BG^0_B+RT\left(X_A\ln{X_A}+X_B\ln{X_B}\right)+X_AX_BI_\text{AB} $$

则$I_\text{AB}$将不再有明确的物理意义，它将不仅负责修正相互作用能，也要修复线性项的偏差. 此时的$I_\text{AB}$更应该叫做相互作用参数(Interaction parameter).

化学势与活度