第一讲 绪论与杆件内力
绪论
基本假设
- 连续性假设
- 均匀性假设
- 各向同性假设
- 小变形假设
外力
按照作用方式分类:
- 体积力
表面力
- 集中力
- 分布力
按照与时间的关系分类:
- 静载荷
动载荷
- 交变载荷
- 冲击载荷
应力
应力从单位上看,不是力。
去除了力的大小对几何尺寸的依赖(截面面积越大,截面总力越大)因此某种程度上可以认为p(压强)等比值定义的量可以认为是某点的该物理量大小- 平均应力$$p_M=\frac{\Delta F}{\Delta A}$$
- 一点的应力(全应力)$$p=\lim\limits_{\Delta A\rightarrow 0}\frac{\Delta F}{\Delta A}=\frac{\rm dF}{\rm dA}$$
通常把应力p分解成切向分量 $\tau$切应力和法向分量 $\sigma$正应力.
应力描述物体强度.
一般(空间)的应力状态
微元体体积无穷小,相对面上的应力等值、反向、共线.
变形、位移和应变
- 变形(deformation)
在外力作用下物体形状和尺寸发生改变 - 位移(displacement)
变形前后物体内一点位置的变化 应变(strain)
度量构件一点处的变形程度- 正应变
线应变(normal strain) $$\epsilon=\lim\limits_{\Delta s\rightarrow0}\frac{\Delta u}{\Delta s}=\frac{\rm du}{\rm ds}$$ - 切应变
剪应变、角应变(shearing strain)单位体相邻棱边所夹直角的改变量
用$\gamma$表示
- 正应变
$\epsilon$描述尺寸的改变,$\gamma$描述形状的改变.
应变量描述物体刚性.
胡克定律
$$\sigma=E\varepsilon$$E称为弹性模量(杨氏模量)
$$\tau=G\gamma$$G称为切变模量(剪切弹性模量)
杆件内力
杆件变形的基本形式
- 轴向拉伸和压缩(axial tension and compression)
力沿轴线 - 剪切(shear)
大小相等,指向相反,作用线距离很近 - 扭转(torsion)
垂直于杆件轴线施加一对力偶 - 弯曲(bending)
在包含杆件的纵向平面内作用一对等大反向的力偶
还有组合变形
截面法
- 1)截
在所求截面处截平面 - 2)取
取一部分作为研究对象 - 3)代
- 4)平
若轴力的指向背离截面,则规定为正,称为拉力(tensile force)
若轴力的指向指向截面,则规定为负,称为压力(compressive force)
轴力图:画出$F_N-x$图像
从已知出发,按照方法列方程
扭转
$$M_e\ \omega=M_e\times\frac{2\pi n}{60}=P\rm(kW)$$
$$M_e=9549\frac{P}{n}\rm(N\cdot m)$$
弯曲
直杆受的外力是垂直于轴的平衡力系,变形后杆轴变为曲线,这种变形称为弯曲.
以弯曲为主要变形的直杆称为梁.
当梁上所有外力均作用在纵向对称面内时,这种弯曲称为对称弯曲.
支座约束力可以根据静力平衡方程求出的梁称为静定梁.
- 简支梁
一端为固定铰支座,一端为可动铰支座 - 悬臂梁
一端为固定端约束,一端自由 - 外伸梁
固定铰支座和可动铰支座不在梁端
梁在两支座之间的部分称为跨,其长度称为梁的跨长.悬臂梁的跨长是固定端到自由端的距离.
剪力和弯矩
若剪力使$\rm dx$微端的左端对右端向上相对错动,则截面上的剪力为正;反之为负.
剪力方程与弯矩方程
$$F_s=F_s(x),\quad M=M(x)$$
分段画图
若载荷为集中力或集中力偶,则图中有突变,x取值不能等于突变点
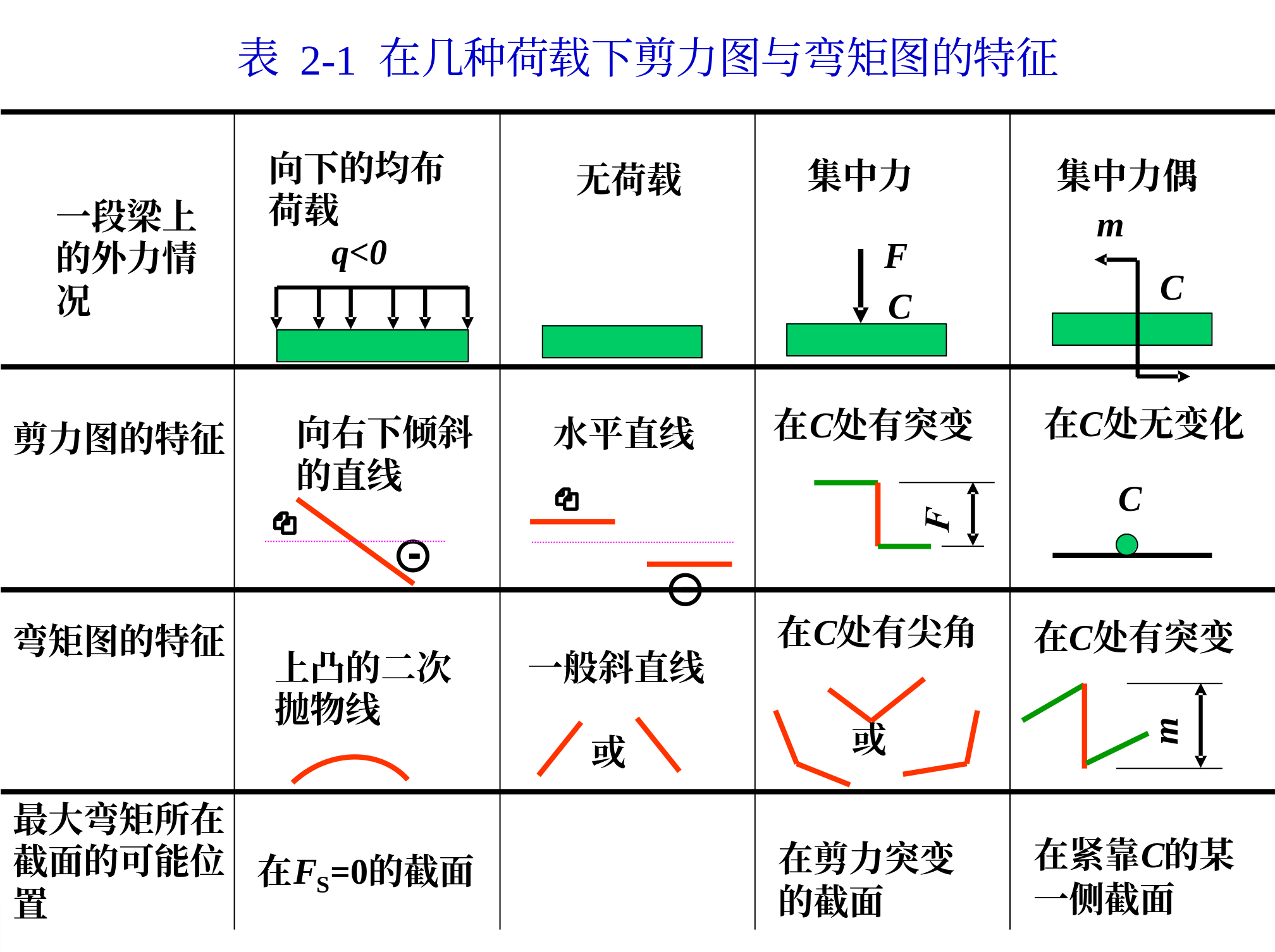
$$\frac{{\rm d}F_s(x)}{{\rm d}x}=q(x),\quad \frac{{\rm d}M(x)}{{\rm dx}}=F_s(x),\quad \frac{{\rm d^2}M(x)}{{\rm d}x^2}=q(x)$$
评论区(暂无评论)