第2讲 晶体结构与空间点阵
固体材料的分类
- 晶体
crystal - 非晶体
amorphous - 准晶
quasicrystal
自然界中绝大部分固体材料都是晶体
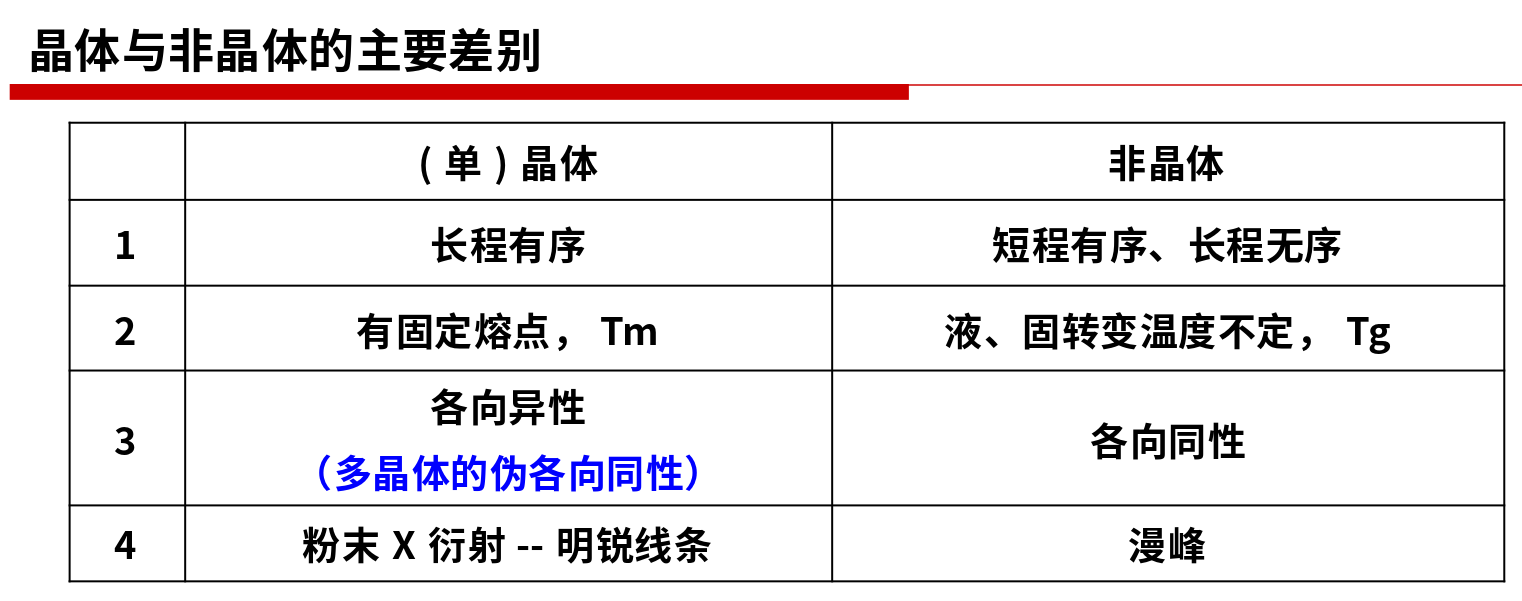
晶体的特点
- 最基本特性:周期性
- 质点
原子、分子、离子、或原子基团在三维空间按一定规律作周期性重复排列的固体 - 长程有序,各向异性
- 遵循面角守恒定律
同物质的不同晶体,在同一温度和压强下,对应晶面之间的夹角恒定。
不能从化学成分或宏观上判断是否为晶体
晶体
晶体的宏观特征
- 自范性
适宜条件下具有自发形成封闭的凸几何多面体外形能力的性质
原因:晶体的生长速度在不同方向上存在差异 - 各向异性
晶体内部各方向有序排列多晶体存在伪各向同性 - 均匀性
宏观上任一部位具有相同的理化性质 - 对称性
理化性质在不同方向或位置上有规律的重复出现
由于有三维周期性的制约,晶体中旋转对称轴次只能有1、2、3、4、6 - 稳定性
晶体具有最小的内能和最大的稳定性
结构基元与阵点
概念
实际晶体中,在空间排布上每隔相同距离重复出现的微粒称为结构基元,简称基元(unit/element/motif/basis)。结构基元这个概念的含义包含原子/分子的种类、数量及其排列方式,可以是单个原子/分子,也可以是在空间以一定方式排列的原子群/分子群
将各种不同的微粒抽象成一个个无体积的几何质点,而完全忽略其物质性,这种抽象的几何质点称为阵点(lattice point)或结点(node)。
构成实际晶体的微粒/结构基元(按一定几何规律周期性排布的原子、分子、离子或原子集团)的具体排列方式称为晶体结构或晶体点阵。
由阵点在三维空间构成的无限阵列称为空间点阵(space lattice),也称空间格子。
空间点阵的两个主要特征:
- 所有阵点都是等同的,都处于相同的周围环境
- 阵点的排列具有周期性。连接任意两个阵点构成一矢量(点阵矢量),按此矢量进行平移,均能使点阵复原(平移对称性)
$$ 晶体结构\quad =\quad结构基元\quad +\quad空间点阵 $$
把空间点阵中的阵点用假想的三组不共面的直线连接起来所构成的空间格架称为晶体格子,简称晶格
- 连接空间点阵中任意两个阵点构成的矢量称为点阵矢量
- 每个方向上连接相邻阵点的矢量称为该方向的基矢(单位矢量)
- 相邻阵点间的距离(基矢长度)称为该方向上晶体的周期
晶胞(cell):从晶格中取出来、能完全反映晶体特征(周期性和对称性)的最小几何单位平行六面体
- 晶胞在三维空间的重复堆垛即构成空间点阵
晶胞的选取既要考虑周期性,又要考虑宏观对称性
- 能代表整个空间点阵的周期性和对称性
- 相等的棱和角的数目最多
- 棱间的直角最多
- 在满足上述条件下,晶胞应具有最小的体积
晶胞的分类
两类晶胞:
- 点阵晶胞:仅反映点阵的周期性,体积最小,但不一定反映对称性,只包含一个阵点,也叫初基胞、固体物理学原胞(Primitive cell)
- 结构晶胞:具有较高对称性的最小重复单元,既反映周期性,也反映对称性,但不一定是最小体积的。也叫结晶学原胞。
另一种分类:
- 简单晶胞: 也称初级晶胞、素晶胞(符号P)
在平行六面体的八个顶点上各有八分之一个阵点,故每个简单晶胞只含有一个阵点。是晶体微观空间中的最小单位,不可能再小。 - 复合晶胞:也称非初级晶胞、复晶胞。复晶胞是素晶胞的多倍体。
除在平行六面体八个顶点上有阵点外,体心(2倍体,符号为I)、面心(4倍体,符号为F)和底心(2倍体)上也有阵点,每个复合晶胞中含有一个以上阵点。
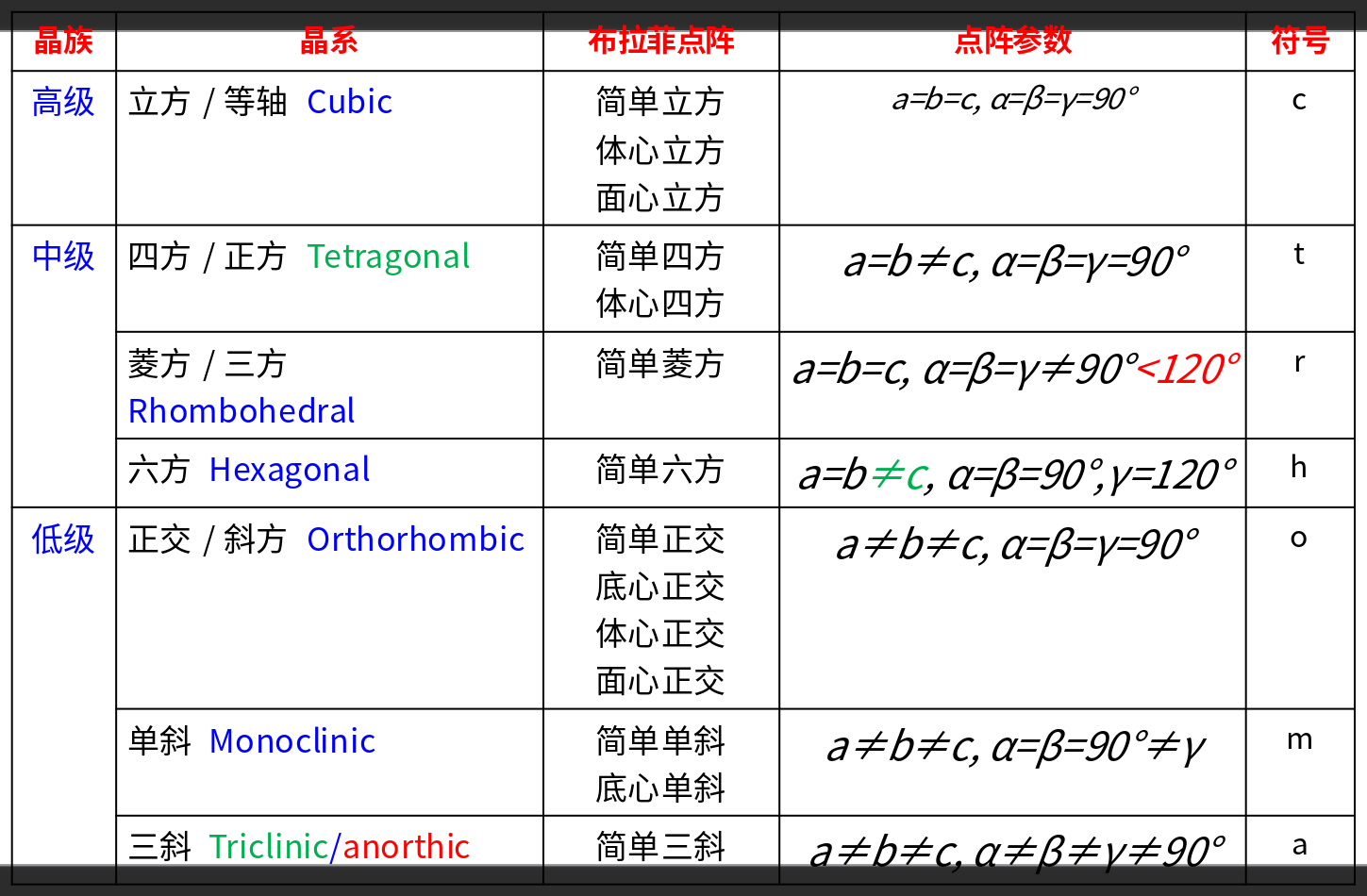
布拉菲点阵
布拉菲依据晶格特征参数之间关系的不同,把14种空间点阵划归为7类,即7个晶系
- 7个晶系的划分依据的是晶体外形的对称,即宏观对称性,是有限大小宏观物体具有的对称性
- 14种布拉菲空间点阵的划分依据的是晶体内部结构基元排列的对称性,即微观对称性,是无限晶体结构具有的对称性
评论区(暂无评论)